5.1. Plot time series

Let us come back to Currency dataset and improve the quality of its visualization.

Currency = read.table("http://edu.sablab.net/data/txt/currency.txt",header=T,as.is=T)

First, we can initialize graphical window using x11().

Please run line-by-line:

x11()  # try x11(width=8, height=5)

plot(Currency$EUR, pch=19, col = "blue", cex=2)

# pre-defined colors in R
colors()

# custom transparent color in #RRGGBB format:
plot(Currency$EUR, pch=19, col = "#00FF0033", cex=2)

There are many graphical parameters which you can tweak using par() functions. Please, have a look by ?par

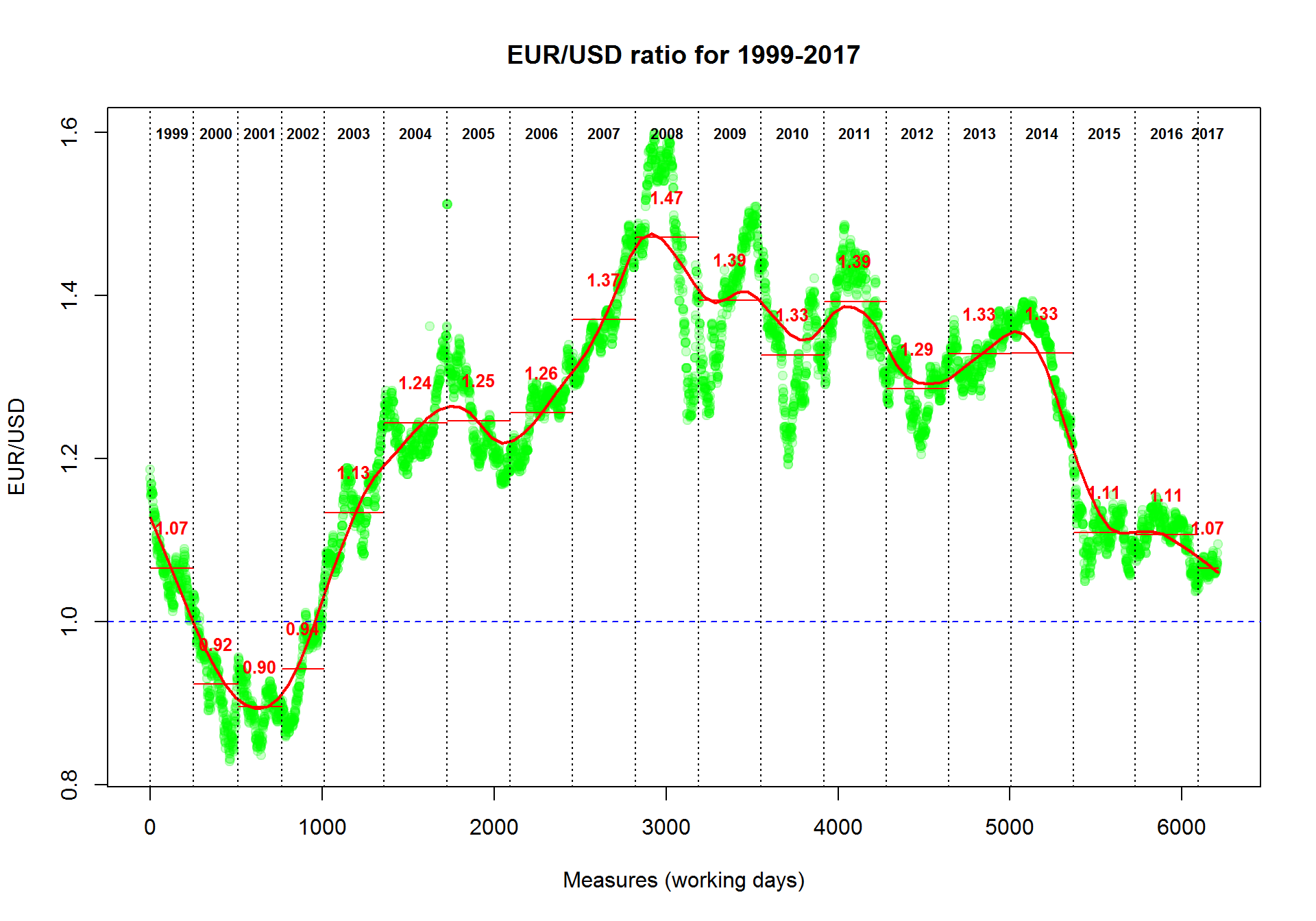
Now we will produce a more plot with smoothed interpolation and average rate for each year. We will add lines to existing plot using lines() and abline() functions. text() will write some text on the plot.

plot(Currency$EUR,col="#00FF0033",pch=19,
     main="EUR/USD ratio for 1999-2017",
     ylab="EUR/USD",
     xlab="Measures (working days)")

## add smoothing. Try different "f"
smooth = lowess(Currency$EUR,f=0.1)
lines(smooth,col="red",lwd=2)
## add 1 level
abline(h=1,col="blue",lty=2)

## (*) add years
year=1999  # an initial year
while (year<=2017){  # loop for all the years up to now
  # take the indexes of the measures for the "year"
  idx=grep(paste("^",year,sep=""),Currency$Date)  
  # calculate the average ratio for the "year"
  average=mean(Currency$EUR[idx]) 
  # draw the year separator
  abline(v=min(idx),col=1,lty=3)  
  # draw the average ratio for the "year"
  lines(x=c(min(idx),max(idx)),y=c(average,average),col=2)  
  # write the years
  text(median(idx),max(Currency$EUR),sprintf("%d",year),font=2,cex=0.7) 
  # write the average ratio
  text(median(idx),average+0.05,sprintf("%.2f",average),col=2,font=2,cex=0.8) 
  year=year+1;
}

5.2. Visualize categorical data

Here we will work with a dataset from Mouse Phenome project. ‘Tordoff3’ dataset was downloaded and prepared for the analysis. See the file here: http://edu.sablab.net/data/txt/mice.txt

Let’s first load the data.

Mice = read.table("http://edu.sablab.net/data/txt/mice.txt", header=T, sep="\t")
str(Mice)
## 'data.frame':    790 obs. of  14 variables:
##  $ ID                  : int  1 2 3 368 369 370 371 372 4 5 ...
##  $ Strain              : Factor w/ 40 levels "129S1/SvImJ",..: 1 1 1 1 1 1 1 1 1 1 ...
##  $ Sex                 : Factor w/ 2 levels "f","m": 1 1 1 1 1 1 1 1 1 1 ...
##  $ Starting.age        : int  66 66 66 72 72 72 72 72 66 66 ...
##  $ Ending.age          : int  116 116 108 114 115 116 119 122 109 112 ...
##  $ Starting.weight     : num  19.3 19.1 17.9 18.3 20.2 18.8 19.4 18.3 17.2 19.7 ...
##  $ Ending.weight       : num  20.5 20.8 19.8 21 21.9 22.1 21.3 20.1 18.9 21.3 ...
##  $ Weight.change       : num  1.06 1.09 1.11 1.15 1.08 ...
##  $ Bleeding.time       : int  64 78 90 65 55 NA 49 73 41 129 ...
##  $ Ionized.Ca.in.blood : num  1.2 1.15 1.16 1.26 1.23 1.21 1.24 1.17 1.25 1.14 ...
##  $ Blood.pH            : num  7.24 7.27 7.26 7.22 7.3 7.28 7.24 7.19 7.29 7.22 ...
##  $ Bone.mineral.density: num  0.0605 0.0553 0.0546 0.0599 0.0623 0.0626 0.0632 0.0592 0.0513 0.0501 ...
##  $ Lean.tissues.weight : num  14.5 13.9 13.8 15.4 15.6 16.4 16.6 16 14 16.3 ...
##  $ Fat.weight          : num  4.4 4.4 2.9 4.2 4.3 4.3 5.4 4.1 3.2 5.2 ...

If you would like to have an overview of the data, and you have a reasonable number of columns, you can just plot() all possible scatter plots for your data.frame

plot(Mice, pch=".", col="blue")

Let us plot some factorial data. For example, we can check how well was the experiment designed with respect to mouse strain.

plot(Mice$Strain)

Or do it more beautifully:

plot(Mice$Strain, las=2, col=rainbow(nlevels(Mice$Strain)), cex.names =0.7)
title("Number of mice from each strain")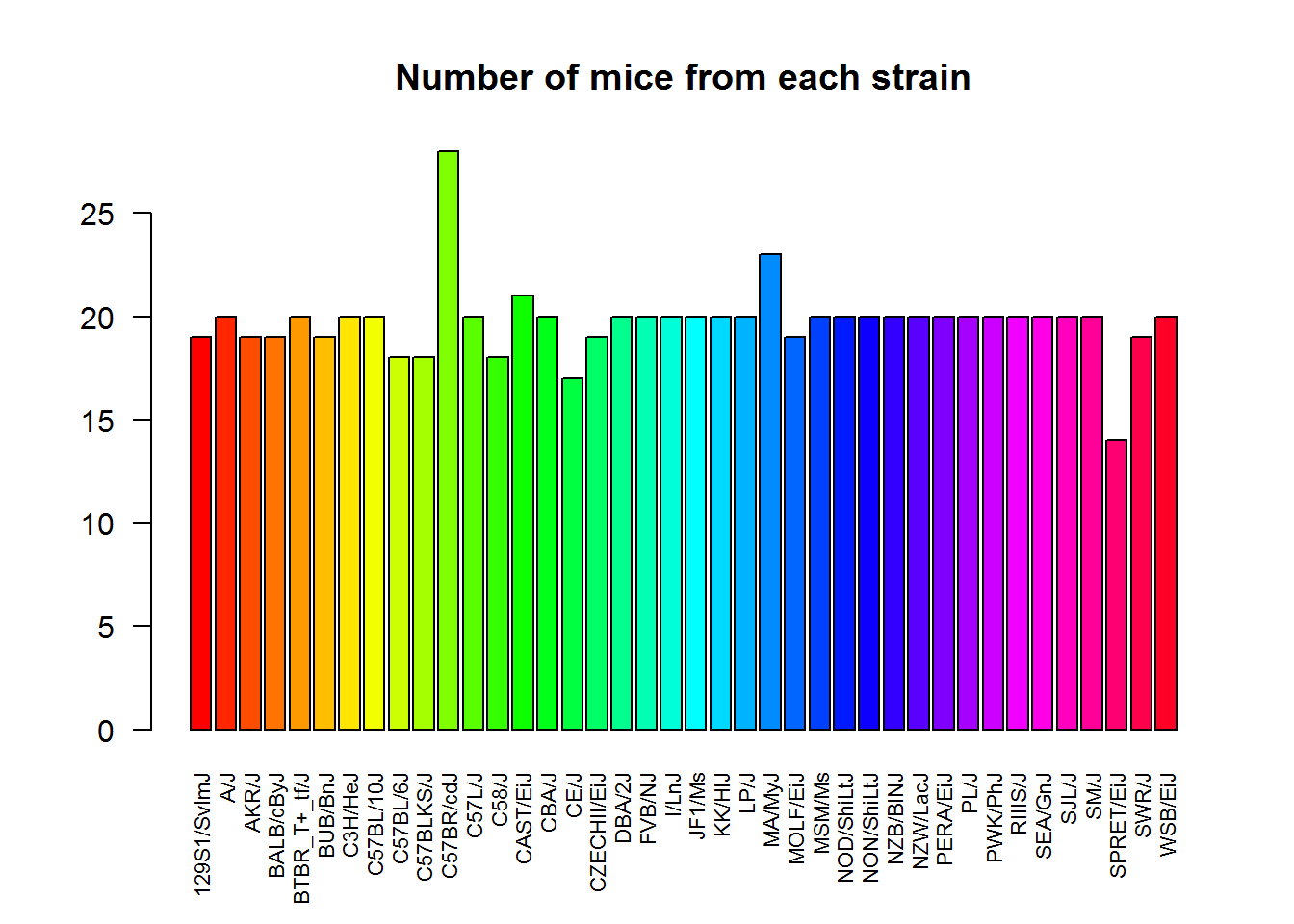

Pie-chart

pie(summary(Mice$Sex), col=c("pink","lightblue"))
title("Gender composition (f:female, m:male)")

5.3. Distributions and box-plot

Distributions can be shown using hist() or plot(density()) functions.

hist(Mice$Starting.weight,probability = T, main="Histogram and p.d.f. approximation", xlab="weight, g")
lines(density(Mice$Starting.weight),lwd=2,col=4)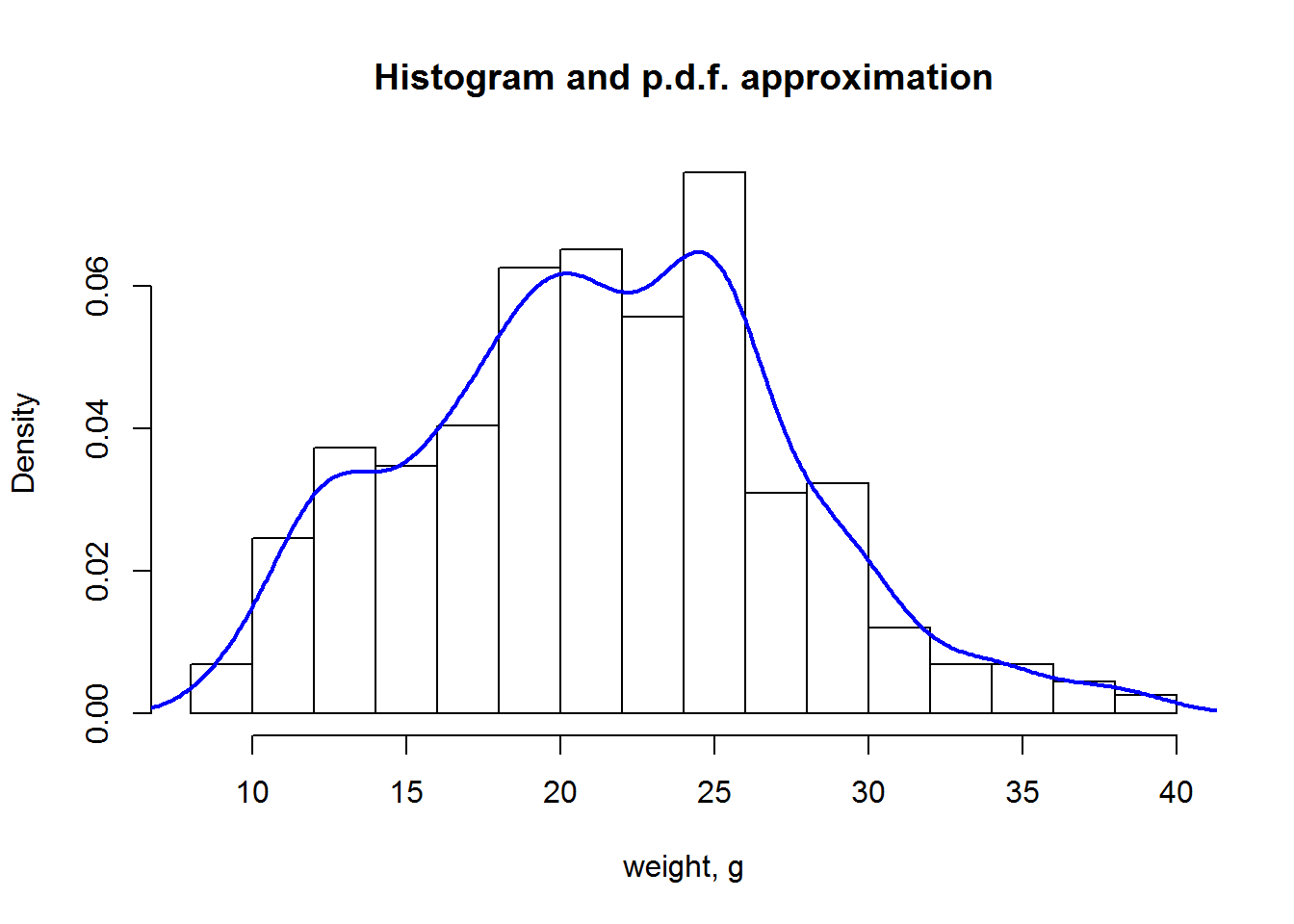

Now let us build a standard boxplot that shows starting weight for male and female mice. We will use formula here: ‘variable’ ~ ‘factor’. It is the easiest way.

boxplot(Starting.weight ~ Sex, data=Mice, col=c("pink","lightblue"))
title("Weight by sex (f:female,b m:male)",  ylab="weight, g",xlab="sex")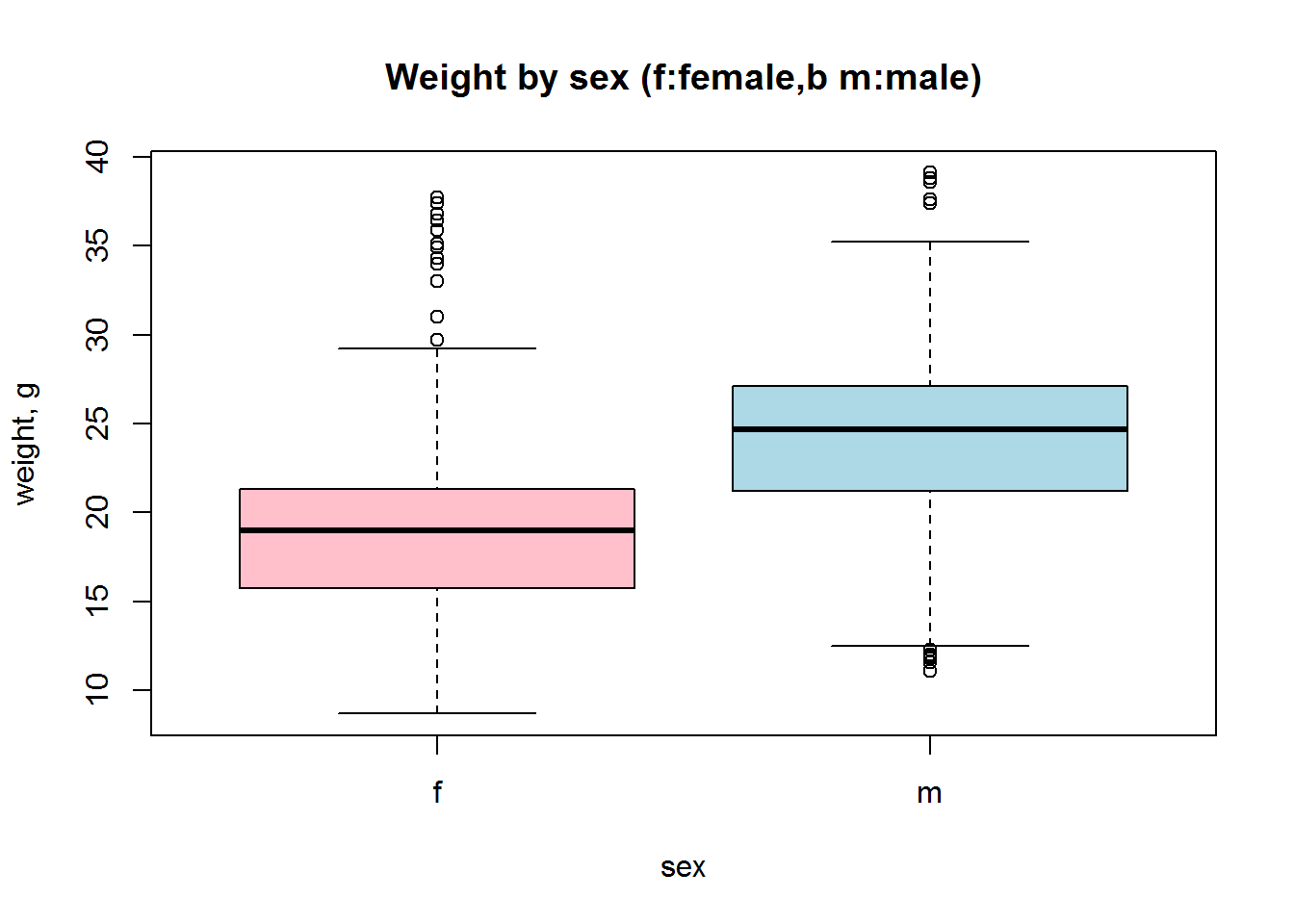

5.4. Heatmaps

Heatmaps are a useful 2D representation of the data that have 3 dimensions. Example: expression (dim 1) is measured over n genes (dim 2) in m samples (dim 3). Heatmaps will automatically cluster the data (see Lecture 9). Let us make a heatmap for internal Iris dataset. We should also transform data.frame to a matrix

# see iris dataset
str(iris)

# let us transform the data to a matrix
X = as.matrix(iris[,-5])
heatmap(t(X))

``

# add species as colors
color = as.integer(iris[,5])
str(color)
##  int [1:150] 1 1 1 1 1 1 1 1 1 1 ...
color = rainbow(4)[color]
str(color)
##  chr [1:150] "#FF0000FF" "#FF0000FF" "#FF0000FF" "#FF0000FF" ...
heatmap(t(X),ColSideColors = color)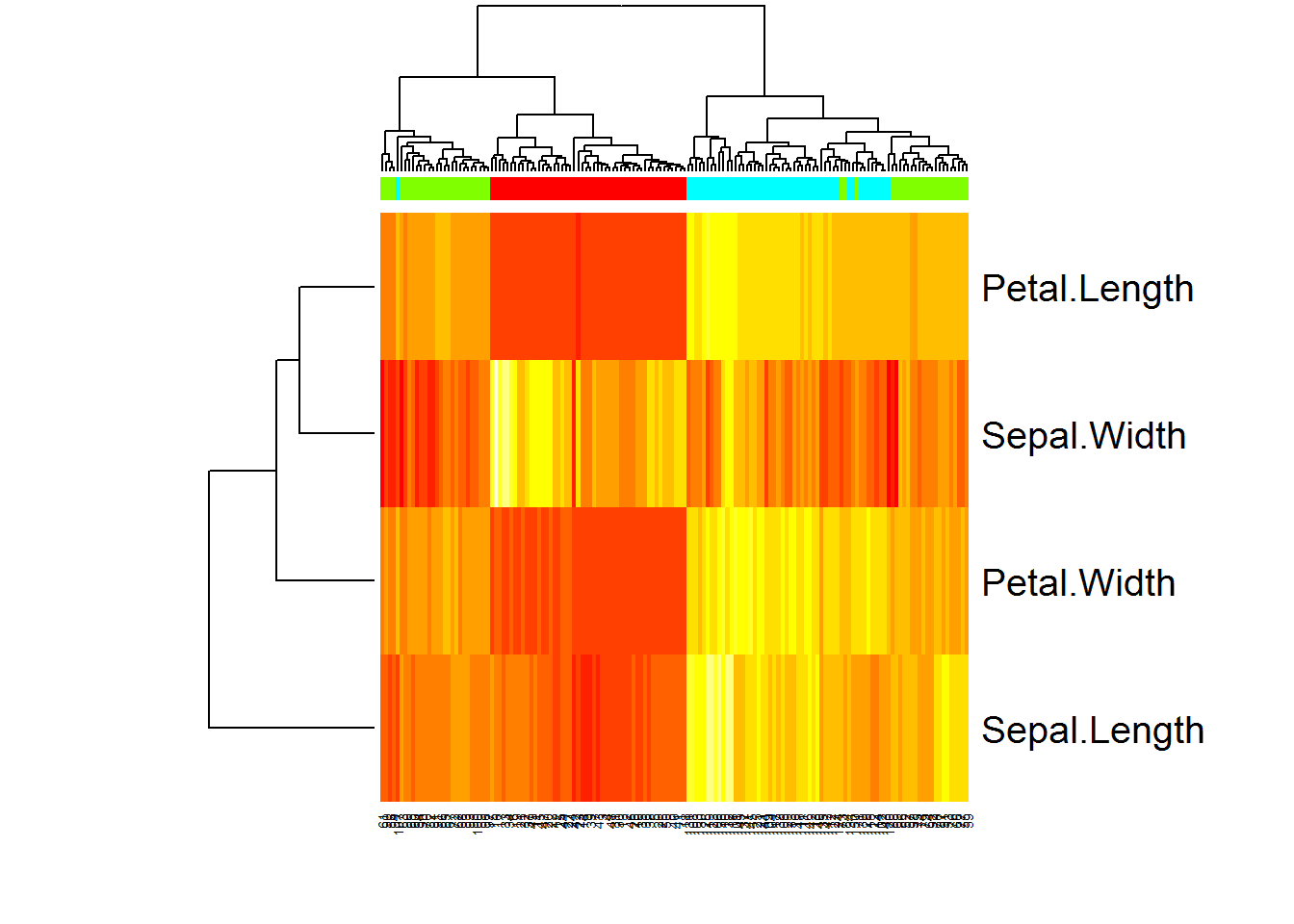

More advanced heatmaps can be built using pheatmap package.

5.5. 3D visualization

There are options for 3D plotting in R. See static images in demo(persp) And here is an interactiv 3D plot using rgl package:

library(rgl)

# define coordinates
x=Mice$Starting.weight
y=Mice$Ending.weight
z=Mice$Fat.weight

# plot in 3D
plot3d(x,y,z)

Exercises

  1. Use mice dataset. Build distributions for male and female body weights in one plot.

plot, density

  1. Draw boxplots, showing variability of bleeding time for mice of different strains.

boxplot

LIH